
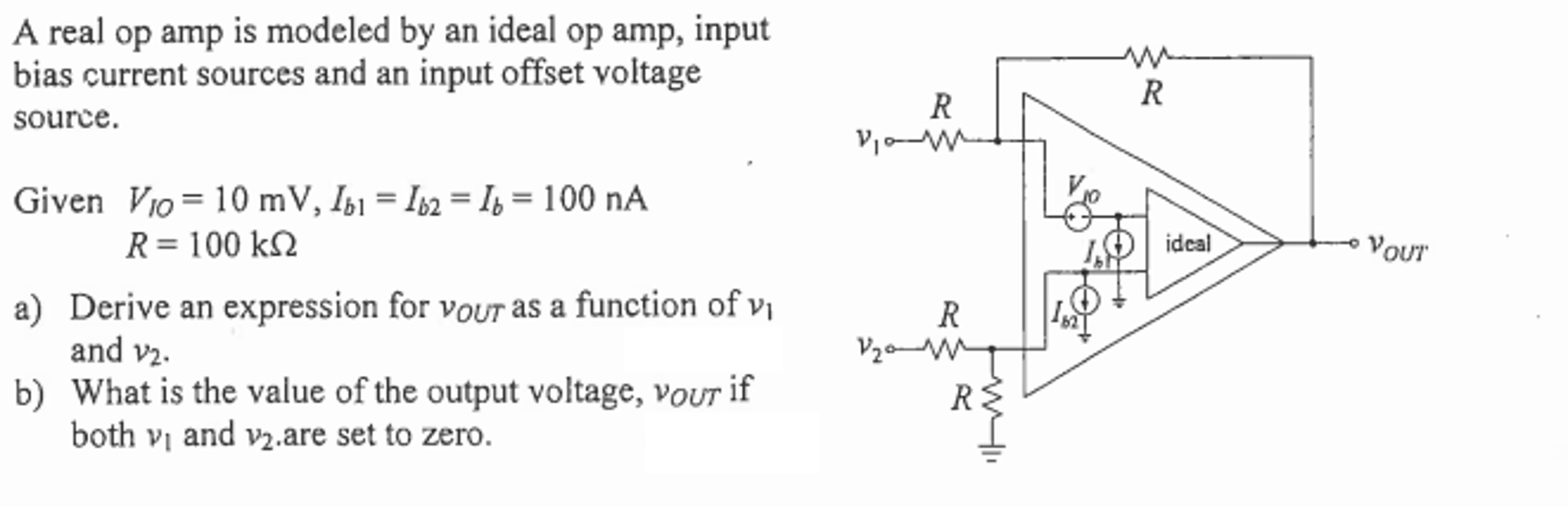
Ibos = Ib1 – Ib2īias Current for CMOS Bias current in MOSFET amplifiers is mainly from leakage into ESD diodes. Note that when this is done, Ib can flow in both directions. This has the effect of significantly reducing input Ib. It is typically larger then FET and it flows into the input terminals.īipolar with Ib Cancelation The input bias currents are mirrored and summed back in to cancel the bias current.

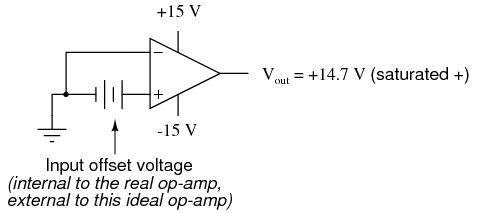
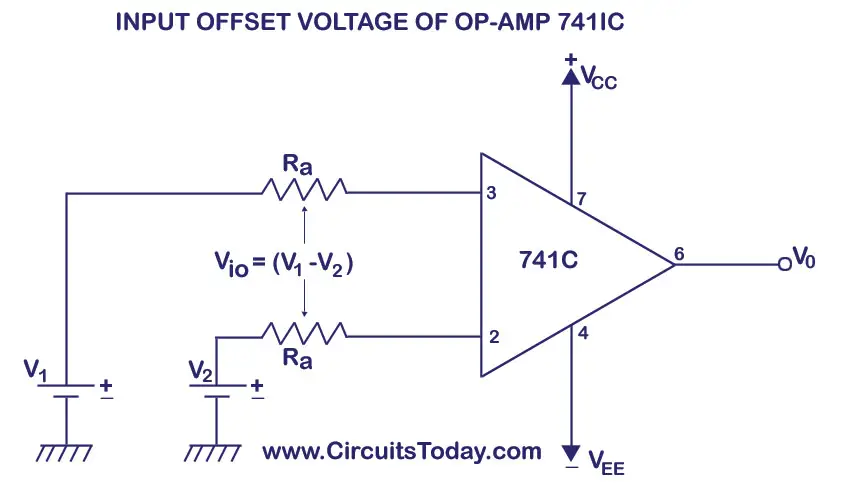
Simple Bipolar (No Ib Cancelation) Bias current in Bipolar amplifiers is from Base Current. Input Bias Current Input offset current: Ibos = Ib1 – Ib2 = 210nA – 150nA = 60nA OPA835 OPA835 Drift Slope – Positive and Negative For this example Vos drift is defined: Let’s start by putting the buffer to good use as an Op-Amp Voltage Reference.Simulate Input Offset VoltageLook at the Test Conditions In the next few sections, we’ll look at alternative configurations: We’ve used an op-amp to build a voltage buffer with voltage gain A v = 1 There’s a better way, covered in a later section!) (Advanced readers note: this is not the best way to use an op-amp and BJT as a precision current source. This alone can be a huge win by making the engineer’s life easier and in making the design more robust to component manufacturing variations. Most importantly, the buffer allows us to isolate different sections of the design: the design choices of R1+R2 are now much more independent from the design choices of Q1+RE. But in many cases, the math works out that this is a winning trade! We also slightly increased the cost and space required by adding a component. By adding the op-amp voltage buffer, we win from the reduced power consumption in R1 and R2, but we lose a bit by adding the new power consumption of the op-amp’s own quiescent current. In the real world, there is a tradeoff to this approach. Now that we’ve added a buffer, how do V outĬhange as we increase the resistance parameter xĪs is quickly evident from the flat DC Sweep simulations, this lets us use much larger resistance values for R1 and R2 (therefore reducing power consumption in the voltage divider) without having any change in LED current! We’ll now calculate the frequency response algebraically using the Laplace transform.Īs shown in the Ideal Op-Amp section, we can model the open-loop transfer function of the ideal op-amp (with finite GBW and A_OL) in the Laplace domain as:Įxercise Click to open and simulate the circuit above. The GBW is listed on an op-amp’s datasheet, so you may be able to solve this problem by simply buying a faster op-amp. ) For signals at frequencies at or above the GBW, the op-amp won’t be able to respond fast enough to copy the signal from input to output. (As a rule of thumb, let’s say you’re reasonably safe if f signal < 1 10 GBW What’s the -3 dB frequency? Double-click OA1, adjust the A_OL, and re-run the simulation: does the Bode plot change? Next, do the same for GBW.Īs shown by this circuit simulation, the -3 dB knee in the frequency response curve happens at the gain-bandwidth product (GBW) of the op-amp.įor practical purposes, this means that we can assume that a real-world op-amp voltage buffer will do its job well for signals with a frequency much lower than the GBW of the op-amp. The voltage buffer circuit is connected so that:Įxercise Click to open and simulate the circuit above.


 0 kommentar(er)
0 kommentar(er)
